This triangle is impossible.
If the distance between B and C is 0, B and C are the same points. If that is the case, the distances between A and B and A and C must be the same.
However, i ≠ 1.
If you want it to be real (hehe) the triangle should be like this:
C | \ |i| | \ 0 | \ A---B |1|Drawing that on mobile was a pain.
As the other guy said, you cannot have imaginary distances.
Also, you can only use Pythagoras with triangles that have a 90° angle. Nothing in the meme says that there’s a 90° angle. As I see it, there are only 0° and 180° angles.
Goodbye, I have to attend other memes to ruin.
Context matters. In geometry i is a perfectly cromulent name for a real valued variable.
Oh shit, he used the word cromulent. Every one copy off this guy.
That wouldn’t be cromulent, would it?
Mad mobile drawing!!
As the other guy said, you cannot have imaginary distances.
Incorrect. There are complex valued metric spaces
And even if we assume real valued metrics, then i usually represents the unit vector (0,1) which has distance real 1.
That’s NOT a metric. That’s a measure. Two wholly different things.
It can be a pseudometric
That’s more related to a metric but it still can’t be complex valued and it’s still not a measure.
This is clearly meant to be a right triangle. And the distances between the points are the same (because the squares of the coordinate differences are the same), just the directions are different.
If you move 1 unit forward, turn the correct 90 degrees, and then move i units forward, you will end up back where you started.
You can’t have a distance in a “different direction”. That’s what the |x| is for, which is the modulus. If you rotate a triangle, the length of the sides don’t change.
The vector from one point to another in space has both a distance (magnitude) and a direction. Labeling the side with i only really makes sense if you say we’re looking at a vector of “i units that way”, and not at an assertion that these two points are a directionless i units apart. Then you’d have to break out the complex norms somebody mentioned.
Isnt it fine to assume a 90° angle its just that when u square side AC ur multiplying by i which also represents a rotation by 90° so u now nolonger have a triangle?
It’s not fine to assume a 90° angle. The distance between B and C is 0. Therefore the angle formed by AB and AC is 0°.
If the angle is 90°, then BC should be sqrt(2), not 0. Since the length of both sides is 1. sqrt(|i|2+|1|2) = sqrt(2).
So essentially what ur saying is. The imaginary and real arent 90° or pythagoras is only valid for real numbers?
1 • 1 + i • i = 1 + (-1) = 0 = 0 • 0
Pythagoras holds, provided there’s a 90° angle at A.
this is why it is still a theorem
I’m so angry at people who think that distances can be imaginary.
Never been together with people and still felt alone?
When talking about AC power, some of the power consumed doesn’t actually produce real work. It gets used in the generation of magnetic fields and charges in inductors and capacitors.
The power being used in an AC system can be simplified by using a right triangle. The x axis is the real power being used by resistive parts of the circuit (in kilowatts, KW). The y axis is reactive power, that is power being used to maintain magnetic fields and charges (in kilovolt-amperes reactive, KVAR). And the hypotenuse is the total power used by the circuit, or KVA (kilovolt-amperes).
Literal side note: they’re all the same units, but the different sides of the triangle are named differently to differentiate in writing or conversation which side of the power triangle is being talked about. Also, AC generator ratings are given in KVA, so you need to know the total impedance of your loads you want to power and do a bit of trig to see if your generator can support your loads.
The reactive component of AC power is denoted by complex numbers when converting from polar coordinates to Cartesian.
Anyways, I almost deleted this because I figured your comment was a joke, but complex numbers and right triangles have real world applications. But power triangles are really just simplifications of circles. By that I mean phasors rotating in a complex plane, because AC power is a sine wave.
By that I mean phasors rotating in a complex plane, because AC power is a sine wave.
I read the entire thing as Air Conditioning and it made me think my tired ass had forgotten something important and then here comes like whiplash when it clicked that you were talking about Alternating Current.
More coffee needed.
Please be careful with two different things. Complex numbers have two components. Distances don’t. They are scalars. The length of the vector
(0,1)is also1. Just asa+biwill have the lengthsqrt(a^2 + b^2). You can also use polar coordinates for complex numbers. This way, you can see thatihas length1, which is the distance from0.The triangle in the example above adds a vector and a scalar value. You can only add two vectors:
(1,0) + (0,1)which results in(1,1)with the proper length. Or you can calculate the length/distance (absolute values) of the complex numbers directly.Its another classic case of Euler’s Identity
They’re about as imaginary as numbers are in general.
Complex numbers have real application in harmonics like electronics, acoustics, structural dynamics, damping, regulating systems, optronics, lasers, interferometry, etc.
In all the above it’s used to express relative phase, depending on your need for precision you can see it as a time component. And time is definitely a direction.
That’s not relevant to what they said, which is that distances can’t be imaginary. They’re correct. A metric takes nonnegative real values by definition
Why can’t a complex number be described in a Banach-Tarsky space?
In such a case the difference between any two complex numbers would be a distance. And sure, formally a distance would need be a scalar, but for most practical use anyone would understand a vector as a distance with a direction.
The distance between two complex numbers is the modulus or their difference, a real number
You’re mad at mathematicians for constructing complex valued metrics? It’s all just formalism, nothing personal.
Omg, yes. This is horrible. :)
But that’s not the definition of the absolut value, I.e. “distance” in complex numbers. That would be sqrt((1+i)(1-i)) = sqrt(2) Also the triangle inequality is also defined in complex numbers. This meme is advanced 4-4*2=0 Works only if you’re doing it wrong.
You didn’t really expect an imaginary triangle to behave like a real one, did you?
I get it, it’s projected on a comlplex sphere. B and C are the same point
please stop making it make sense
C and B have a wormhole between them
In the complex plane each of these vectors have magnitude 1 and the distance between them is square root of two as you would expect. In the real plane the imaginary part has a magnitude of zero and this is not a triangle but a line. No laws are broken here.
i = 1is the only logical choiceLiterally, this is one of those questions where they’re testing logic and your understanding that the figures aren’t necessarily representative of physical reality.
It gets worse once you start doing trig on it
I kept seeing this pop up recently, and I finally understand it: it’s an introductory problem in Lorentzian general relativity.
AB is a space-like line, while AC is a time-like line. Typically, we would write AC as having distance of 1, but with a metric such that squaring it would produce a negative result. However it’s similar to multiplying i to the value.
BC has a distance of 0, but a better way of naming this line would be that it has a null interval, meaning that light would travel following this line and experience no distance nor time going by.
I’m sure PBS Spacetime would explain all of this better than me. I just woke up and can’t bother searching for the correct words on my phone.
Maybe the problem is constructing a metric that makes this diagram true. Something like d(x,y) = | |x| - |y| | might work but I’m too lazy to check triangle inequality.
Triangle inequality for your metric follows directly from the triangle inequality for the Euclidean metric. However, you don’t need a metric for the Pythagorean Theorem, you need an inner product and, by definition, an inner product doesn’t allow non-real values.
Wish me luck for I’m doing trig test with radians (2 pi rad = 360 ?)
Radians are the objectivly better way to do angles tho. Just remeber π=180deg and ur right. Btw here is a another brain fuck the units radians/second is just Hz
Thank you for reminding me!
Btw, Radians/sec = Hz? What is this, physics?
Engineering unit maths. Cos angles are unitless so radians/second =1/second=Hz
The easiest way to think about it is that 1 full rotation (2*pi radians) in 1 second makes 1 Hz.
The number of rotations made in a second corresponds to Hz in the same way that the number of sine wave periods that fit in a second also represents Hz. This gif does a really good job of showing how rotation relates to sine/cosine waves, which just so happens to help visualize the rad/s -> Hz <- periods/s relationship:
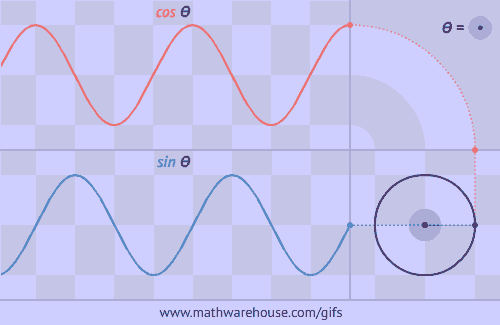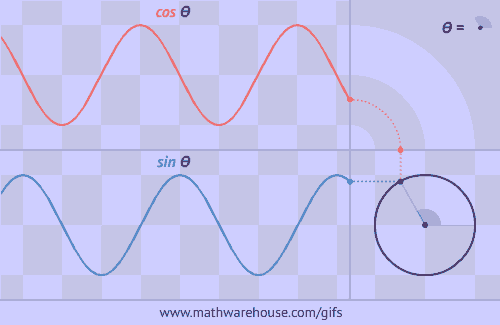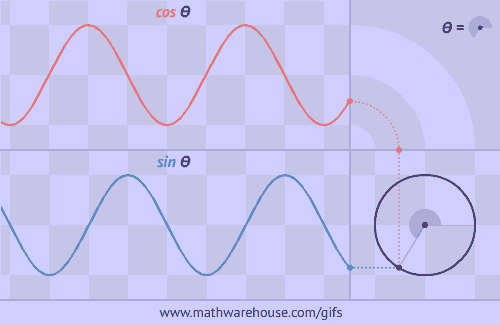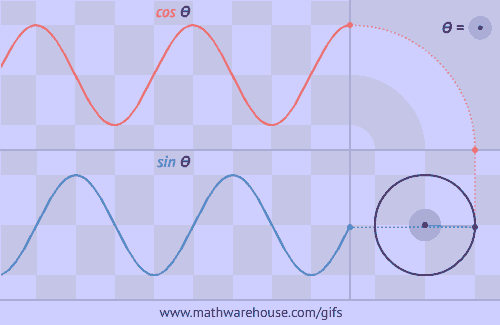
Radians are the objectivly better way to do angles
Yes, and tau is objectively better than pi. Just remember tau = 360°. Which is a full circle, which easier to work with than half a circle.
You can make something like this properly by defining a different metric. For example with metric dl2 = dx2 - dy2 the vector (1, 1) has length 0, so you can make a “triangle” with sides of lengths 1, -1 and 0.
That’s not a metric. In any metric, distances are positive between distinct points and 0 between equal points
It depends which metric definition are you using. The one I wrote is a pseudo-Riemannian metric that is not positive defined.
Normally physicists use that generalized metric definition because spacetime in most cases has a metric signature of (-1, 1, 1, 1). Points with zero distance are not necessarily the same point, they just are in the same null geodesic.
You’re talking about a metric tensor on a pseudo-Riemannian manifold, I’m talking about a metric space. A metric in the sense of a metric space takes nonnegative real values. If you relax the condition that distinct points have nonzero distance, it’s a pseudometric.
This is true for real-valued metrics but not complex-valued metrics.
Metric, not measure. Metrics are real by definition.
funny Interpretation: in the complex plane, the imaginary axis is orthogonal to the real axis. so instead of the edge marked with i (AC), imagine an edge of length 1 orthogonal to that edge. It would be identical to AB, so
ACCB is 0.But then CB couldn’t also be 0; wouldn’t it be
cos(1 + i)? Or something like that.oh I mixed up the points, I meant to say CB is 0 in the end
I feel violated trying to read that in my brain.
Uhh 21?













