So I found out about Marx’ mathematical manuscripts, so I say “Hey, I’ve been studying mathematics this year at university. I understand limits and derivatives, maybe I can understand something of that gibberish.” So I see the titles and the one called “On the Concept of the Derived Function”, I go there and I see some notation I don’t understand, he speaks about things I’m not clearly understanding, so maybe some of you could make it clear.
For example:
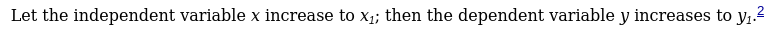
Why is this x sub 1 notation? Is this some other way to write derivatives? Because on the footnotes it says this:
- In order to avoid confusion with the designation of derivatives, Marx’s notation x´, y´, … for the new values of the variable has been replaced here and in all similar cases by x1, y1, …
Then I saw a talk about Marx’s mathematics and the infinitesimal and some of that stuff, but the one who was speaking didn’t went much into the mathematical part but was more like a history talk on how the Chinese were interested in the propositions of Marx because it liberated calculus from the idealist veil with which it was conceived by Leibniz and Newton, but the one who was talking mentioned Marx learning mathematics with whatever he had around and didn’t managed to read Cauchy so we was like “Yeah this is nice but it’s al shit now we have proved it fully works.” But well, he seems a bit biased, since he’s a Usonian, so maybe Marx’s writings are still relevant, I don’t even know who the fuck Cauchy is, so yeah, help.
Text: https://www.marxists.org/archive/marx/works/1881/mathematical-manuscripts/ch03.html
Just wanted to say thanks for bringing up this topic and thanks to those who have commented. Fascinating topic. I am not a mathematician, but you have asked and answered questions so clearly that I have understood what you’re saying.
Although there seems to be some debate about his politics, Lancelot Hogben was a materialist who wrote Mathematics for the Million: How to Master the Magic of Numbers. In the ‘Instructions for Readers of this Book’, he wrote:
The customary way of writing a book about mathematics is to show how each step follows logically from the one before …. This book … show[s] how each step follows historically from the step before ….
The book as a whole gives a
bird’s-eye view of the social interconnections of mathematics[.]
To me, if a materialist writes a book to put a subject in it’s historical context, to explain social interconnections, they are more or less an historical materialist, i.e. a Marxist, who wants to do Marxism in the West, in the height of the cold war, without losing their job.
Anyway… you might find the book helpful. I have only read the first couple of chapters. I found it interesting, although you appear to be far more advanced than I am. It is the kind of book that you can just read and enjoy from start to finish, but there are exercises, too. Hogben suggests reading it once to understand the structure, then a second time more carefully and to complete the exercises.
There is a pdf on the internet if you search for it in the usual places. It may be too basic for you, but it seems to be in-depth to me.
Thanks a lot for your recommendation, I have again add it to my infinite to read list, and while I’m currently reading like 4 books at the same time I will try to make room for it this year, since it seems like an interesting book which can help me understand mathematics better which comes in hand for the university. I wouldn’t call myself much more advanced, limits and derivatives seem like a complex and smartsy pantsy subjects but they are not that hard to understand if you have the correct person to explain it to you and you have some other basic knowledge of mathetmatics. Thanks again, comrade!
Where would we be without infinitely growing reading lists? You’re welcome.
I’d love to read a breakdown thread of this text if u ever fully detangle it. Maybe u could apply the same critical logic to Cauchy that Marx applies to earlier theorists.
I feel like the “standard model” of any field of science on some level betrays the often limiting assumptions foundational to that field, which makes a historical materialist approach to mathematics very intriguing. How to model change, whether mathematically or socially, is a very philosophical question.
Well, really, really, really rough tl;dr, but basically Marx writings still hold up in some way, Cauchy formalized Leibniz/Newton theory, derivatives are still a somewhat shady mathematical subject which nevertheless provides good results in praxis.
Marvel at Marx’s Most Meticulous Mathematical Manuscripts
Why do you say that? Do you think they are too badly written?
just alliteration, what I read (part 1) makes perfect sense
What do you mean by alliteration? Well, yes, it does, but I don’t know how much of this still holds up to today, that was mostly my doubt, since apparently this guy Cauchy provided a more rigorous definition of the derivatives than Leibniz/Newton which Marx was criticizing here. Basically Marx here is doing some work understanding the differences as the dialectical change in mathematics, but I don’t know, really.
Alliteration is when you use several words next to each other that start with the same consonant.
Hey there. I suppose that people would refer to me as a Mathematician, so I might be able to help clarify a few things for you! One thing I’d like to add is that it’s exciting to see other people looking into this stuff because it’s something of a huge project of mine now to try to understand dialectical materialism as an epistemological theory as well as how it then relates to mathematics and science, where we are often wondering how we develop “mathematical” or “scientific” knowledge.
First off, other posters here are correct about the subscripts, what Marx is referring to is just the simple idea that if
yis defined so that it depends onxthen when you changexyou’ll get a corresponding change inybased on howyis defined. For example if we define a functiony = x + 1then say x = 0 and x1 = 1 then the corresponding values forywhen we plug in these values of x would be y = 1 and then y1 = 2. Here we can see that we changedxby 1 and we got out a corresponding change inyof 1. The ratio then would be1/1or simply 1. If you’re familiar with Calculus then the derivative of that functiony = x + 1yieldsdy/dx = 1and indeed if you check the ratio between the change inxand the corresponding change inyfor any values ofxandyyou will always get 1 for this exact function.As for the second part of your question: The history of mathematics here is interesting, and to cut to the chase a bit, Leibniz and Newton both actually use the infinitesimal (denoted most commonly as
dxordyin Mathematics textbooks today) in the development of Calculus. All this infinitesimal is, is a very tiny, basically infinitely tiny small change in the value forxoryrespectively ( any mathematicians out there: do not attack me). At that time there was no need for these incredibly logically precise mathematical objects because mathematics was not developed the same way it is today and so “proof” was a lot less formal than it is today (and in-fact, proof today is even not as formal and formalists would like it to be).The issue with Leibniz and Newton’s conception of the infinitesimal was that it was a rather “qualitative” development of the previous work done on this by the Greek mathematician Archimedes, and in a field highly concerned with quantitative descriptions… “How could we just say this derivative function use a non-numerical value
dxto denote a small change inxand call that proof when we have Archimedes”? And this question plagued mathematics for years and years and really got very messy because this just couldn’t continue for the mathematicians at that time, in fact some people at that time didn’t even consider the work of Leibniz or Newton to even be “mathematics”. However the work being done using this stuff by physicists was incredible, we developed very complex machinery and harnessed electricity all using this “infinitesimal” and the results were incredibly accurate to physicists observations. So it certainly couldn’t be thrown out.During the mid - 1800’s, mathematics was unsurprisingly developing very rapidly (And this is no accident! Rapid industrialization led to rapid developments in science and technology and more fertile ground for mathematics to develop, as is the case throughout all of history in fact!).
At this time in Europe, there were two great “schools” of thought about mathematical knowledge, the intuitionists and the so-called formalists, and they wanted to create logically precise ways of doing mathematics and well… the formalists basically won out. So then work was done to “formalize” the infinitesimal and that is where the work of Cauchy came in to formalize this by eliminating the infinitesimal and transforming that idea into a logical structure using “set-theoretical logic”. But simply put, this became the formalist version of the infinitesimal. This is the “standard” idea that we use even unto today and it is known as the limit definition of the derivative.
What you refer to when you mention a talk you saw is the lecture given by Joseph Dauben titled “Marx, Mao, and Mathematics: The Politics of Infinitesimals”. To cut to the chase on this a bit, Dauben mentions that during the cultural revolution, mathematicians were having a very hard time justifying their work within the greater priority of cultural revolution at that time. While I agree that Dauben seems a little confused about Marxism at times in the lecture, I do not believe Dauben is stretching the truth at all here regarding mathematicians in China during this time period because there is a letter that Deng wrote after the cultural revolution titled “Some Comments On Work In Science and Education” where he essentially summarizes how the cultural revolution set China back in science and mathematics.
However, shortly before the Cultural Revolution a mathematician named Abraham Robinson worked on formalizing the notion of an infinitesimal in its own right. His work culminated in the development of a version of Analysis (aka. Calculus) which used this infinitesimal to create something called “Nonstandard Analysis” and so, Dauben comments in that lecture that it was this development of “Nonstandard Analysis” and the Mathematical Manuscripts that allowed some mathematicians in China to continue to work so long as they could show how their work related to Dialectical Materialism or Marxism in some way. Dauben also comments that this has essentially been given up in the years following the Cultural Revolution and indeed that largely is the case, although some Chinese mathematicians do work on Nonstandard Analysis today.
If you have any follow up questions or if any of this piques your interest, I’m happy to continue elaborating on things or helping you during your reading of Marx’s notes on calculus. I honestly have so much to say about this intersection between the dialectics of hegel, dialectical materialism, science, mathematics, Soviet mathematics, etc. that I could probably write a book on it all, if I had time to do it in between work. Luckily small posts like these are much more manageable! Until then, hope this provided the insight that you were looking for!
First off, other posters here are correct about the subscripts, what Marx is referring to is just the simple idea that if y is defined so that it depends on x then when you change x you’ll get a corresponding change in y based on how y is defined. For example if we define a function y = x + 1 then say x = 0 and x1 = 1 then the corresponding values for y when we plug in these values of x would be y = 1 and then y1 = 2. Here we can see that we changed x by 1 and we got out a corresponding change in y of 1. The ratio then would be 1/1 or simply 1. If you’re familiar with Calculus then the derivative of that function y = x + 1 yields dy/dx = 1 and indeed if you check the ratio between the change in x and the corresponding change in y for any values of x and y you will always get 1 for this exact function.
Yeah, I was taught these ideas using different letters for the variables and since I mentioned I am a beginner, I am in my first year of computer engineering so it still takes me some time until I see a formula and get to understand what it’s doing. Basically they taught me what functions are, intervals, inequations, movement of functions in a graph by modifying their variables, limits, derivatives, and function analysis, the subject was called “Introduction to Mathematical Analysis”, so we saw algebra, calculus, but not as individual subjects so yeah, I still need more practice but I think I get the idea here.
As for the second part of your question: The history of mathematics here is interesting, and to cut to the chase a bit, Leibniz and Newton both actually use the infinitesimal (denoted most commonly as dx or dy in Mathematics textbooks today) in the development of Calculus. All this infinitesimal is, is a very tiny, basically infinitely tiny small change in the value for x or y respectively ( any mathematicians out there: do not attack me). At that time there was no need for these incredibly logically precise mathematical objects because mathematics was not developed the same way it is today and so “proof” was a lot less formal than it is today (and in-fact, proof today is even not as formal and formalists would like it to be).
Ahhh, so the dx and dy basically represent that. Yes, we saw this, this is what happens when you divide by a number infinitely closer to 0 which, if it is positive, results in a positive infinite, and if it is negative gives you a negative infinite. So basically dx could be something that produces a value like 00000000000000000000000.1 for example? Of course this could keep getting closer to 0 till infinity. And yeah, this is basically the same method to apply in physics to calculate the average velocity of a particle, only there you usually work with more tangible spaces (meters, centimeters, instead of abstract ideas of infinite), but it basically comes down to calculating the difference in change from one point to the other from both axis.
The issue with Leibniz and Newton’s conception of the infinitesimal was that it was a rather “qualitative” development of the previous work done on this by the Greek mathematician Archimedes, and in a field highly concerned with quantitative descriptions… “How could we just say this derivative function use a non-numerical value dx to denote a small change in x and call that proof when we have Archimedes”? And this question plagued mathematics for years and years and really got very messy because this just couldn’t continue for the mathematicians at that time, in fact some people at that time didn’t even consider the work of Leibniz or Newton to even be “mathematics”. However the work being done using this stuff by physicists was incredible, we developed very complex machinery and harnessed electricity all using this “infinitesimal” and the results were incredibly accurate to physicists observations. So it certainly couldn’t be thrown out.
So this theory proposed by L/N was considered flawed because dx/dy is not actually a numerical value but rather an idea, which can’t be hard proofed. That’s why Engels says this:


Because basically the theories proposed by them wasn’t hard proofed because you were not dealing with numbers but with abstract ideas.
I understand that Archimedes kind of got the idea of the infinite series, do you mean that?
If you have any follow up questions or if any of this piques your interest, I’m happy to continue elaborating on things or helping you during your reading of Marx’s notes on calculus. I honestly have so much to say about this intersection between the dialectics of hegel, dialectical materialism, science, mathematics, Soviet mathematics, etc. that I could probably write a book on it all, if I had time to do it in between work. Luckily small posts like these are much more manageable! Until then, hope this provided the insight that you were looking for!
Well, my main doubt was how much of this texts by Marx still hold up, because from Dauben’s talk it makes it seem as if after Cauchy’s they would have become obsolete and if Marx’s work on calculus and Cauchy’s works contradict each other or if they are compatible. Moreover, would these manuscripts an attempt by Marx to formalize the infinitesimal previously or contemporaneously to Cauchy? Because I think Cauchy’s works were available while Marx was alive but he didn’t managed to read them. And one more question, is there some relation between all this and the idea by Newton that space and time are unrelated as stated in the picture below?

I am truly seriously graceful for your help and your time, you helped me out and while my understanding of these topics is still bland and imperfect I feel I get a better grasp than before. Welcome to Lemmygrad, by the way, hope you are liking it so far!
As a bit of an organizational note, I will be making the primary effort to answer your primary question, and then afterwards I’ll be jumping around to other parts of your post to answer some of the questions that I saw or reflect on some other miscellaneous things.
So to begin I think here is the best place to start:
Well, my main doubt was how much of this texts by Marx still hold up, because from Dauben’s talk it makes it seem as if after Cauchy’s they would have become obsolete and if Marx’s work on calculus and Cauchy’s works contradict each other or if they are compatible.
So there are a couple questions baked in here but I believe the best way to begin is to just go straight to the conclusion and say that: Marx’s Manuscripts do still hold up because they do indeed capture the fundamental ideas of calculus in a much easier to understand way than the formal axiomatic approach, and a skilled mathematician with enough of an understanding of dialectical materialism could use these manuscripts as a starting off point to attack all of the sorts of “institutionalized” aspects of mathematics as it is done around the world. I’ll say that the western institution of mathematics adopts a philosophy that is grotesquely Liberal, and it’s not easy to see why because there really isn’t a lot of work on Marx and Engels and their commentary on mathematics. I will provide a few extra links at the bottom, if your interested in more on this.
Dauben doesn’t really say that Cauchy and Marx would’ve contradicted each other, it has been a bit of time since I’ve listened to that lecture but the best way I would describe it, would be to say that Cauchy represents the idealist desire of mathematicians (and mathematics as whole) to pull their abstractions out of a box and never return them to the real world. They do not know where the abstractions come from nor do they even know how they got into the box! This is a greater problem with mathematics. But that does not mean that “mathematics” is fake in a sense for example here writes Engels:
The so-called axioms of mathematics are the few thought determinations which mathematics needs for its point of departure. Mathematics is the science of magnitudes; its point of departure is the concept of magnitude. It defines this lamely and then adds the other elementary determinations of magnitude, not contained in the definition, from outside as axioms, so that they appear as unproved, and naturally also as mathematically unprovable. The analysis of magnitude would yield all these axiom determinations as necessary determinations of magnitude. Spencer is right in as much as what thus appears to us to be the self-evidence of these axioms is inherited. They are provable dialectically, in so far as they are not pure tautologies. (Engels, Dialectics of Nature: Notes and Fragments)
Here we see the same attack that any Marxist mathematician should be making against mathematics, and indeed, it is Marx that in a sense does develop some ideas of Calculus which are indeed also proven by formal methods, but without ever using formalism… To sum up what I’m trying to say: the Mathematical Manuscripts hold in them a very distilled example of the methodology of dialectical materialism towards the sciences and mathematics. It’s like having a flake of gold that proves that there is some gold in the hill. Also this manuscript should be used by non-mathematicians to study the exact nature of the methodology that Marx and Engels proposes because it clearly shows how Marx uses the concept of an infinitesimal to inquire about it dialectically and then go on to develop more concepts and so on. It is basically a robust exercise in applying dialectical materialism.
Onto the rest of the post:
Moreover, would these manuscripts an attempt by Marx to formalize the infinitesimal previously or contemporaneously to Cauchy?
I wouldn’t say that Marx appears to be trying to formalize anything, really I think the best characterization would be the one I put forward which is that it really is a very clear window into the mind of Marx on using dialectics to develop ideas in mathematics from very basic observations about the so-called “real” behavior of numbers.
And one more question, is there some relation between all this and the idea by Newton that space and time are unrelated as stated in the picture below?
Well certainly the theory of general relativity that Einstein puts forward does indeed link space and time, and ironically it may have been the most famous contemporary example of the relationship between mathematics and physics, because an area of mathematics called differential geometry was in fact developed ahead of Einsteins work on relativity, which in fact essentially inspired the whole theory. And we indeed do build the differential based on this more “formalized” version in modern mathematics, but I should stress that there is no reason why this same process could not be undertaken to explore differential geometry dialectically. Perhaps even it could be of major benefit towards the synthesis of the two competing theories in physics between relativity and quantum field theory. I believe as well that the part where Mao quotes Lenin is again another example of the dialectical process of development in mathematics and science, where we conceptualize in terms of mathematics and we observe in terms of real measurements, and the mathematics helps to develop our observations, and the observations in turn develop our math, with each getting closer and closer to each other, but ultimately because of how conceptions are just shadows of our interpretation of reality, and so our understanding of each is shaped dialectically but not in the sense of the two coming into one, but in the sense that the one (the thing we would like to know) drives this contradiction between the conceptualizations we make for describing reality in mathematics, and the actual observations of reality in science, and that that contradiction drives each of them forward.
So basically dx could be something that produces a value like 00000000000000000000000.1 for example? Of course this could keep getting closer to 0 till infinity.
So basically
+dxor-dxshould be thought of just a value like 0.00000000…001. It doesn’t really produce any sort of value, it is just a notational piece to denote “an infinitesimal positive or negative nudge in x”. In fact as you continue on there will be lots of these little mathematical notational things that are just there because in some sense they represent mathematical ideas instead of numerical things, and they are more like “the language of mathematics”. Which is itself a whole debate.So this theory proposed by L/N was considered flawed because dx/dy is not actually a numerical value but rather an idea, which can’t be hard proofed. That’s why Engels says this…
Precisely, what Engels gets at there is that mathematicians are doing these operations without any understanding of where they came from. In fact in any college level calculus class, by the end of the 1st semester usually students have completely forgotten how to do even the limit definition of a derivative, let alone the way that that the derivative was developed, because there are all these little tricks and patterns that were discovered that would make this process much quicker to compute by hand (For example: The power rule, the quotient rule etc).
I understand that Archimedes kind of got the idea of the infinite series, do you mean that?
Well Archimedes is really the one who came up with the method of exhaustion, which was later developed into the infinite series, but the main contention to Leibniz and Newton and their infinitesimal from the mathematics community at the time was really that they could use the method of exhaustion and the infinite series to compute very close estimates and that these involved purely numbers, so why bother with this infinitesimal thing that doesn’t even really appear to be mathematics?
I am a beginner, I am in my first year of computer engineering
Honestly it’s very impressive that you have even begun asking the questions at such an early stage. This level of curiosity will absolutely serve you well. I would certainly caution you that the way mathematics is presented at first seems to give it the impression that it is really for calculating numbers that we need in engineering or science. But the reality is that, computers pretty much do all of that for us pretty well. So what actual use is it to learn mathematics? Well, I believe that I’ve made a pretty good case for using towards the dialectical development of knowledge in the total system of science with mathematics playing the role of developing conceptualizations to propel forward the sciences, and using the sciences to propel it forward as well, and that of course can come from an engineer just the same as a scientist. In fact in some sense, engineering is the born synthesis of a mathematician and a scientist, and the first step in orienting scientists and mathematicians towards where they should focus their efforts.
I am truly seriously graceful for your help and your time, you helped me out and while my understanding of these topics is still bland and imperfect I feel I get a better grasp than before. Welcome to Lemmygrad, by the way, hope you are liking it so far!
Oh thank you for the warm welcome. I’ve been a lurker for awhile and always loved the quality of discussions here, so finally decided to make an account. Also at the end of the day we’re both also comrades and are on equal ground, and in a real sense the process of discussion on this has helped me learn about this in deeper ways too, so sincerely thank you for posting this thread. I think it was Fanon who talks about how the teacher is a student and I just just hope that this very long response may be of use to you or anyone else.
Thanks again for your impressive response, sorry for not being able to add much to the beginning of your reply, but I agree completely and this has made me change the way I perceive mathematics, I will try to read these texts as soon as possible to see if I can get a better grasp of mathematics from a dialectical materialist point of view.
Precisely, what Engels gets at there is that mathematicians are doing these operations without any understanding of where they came from. In fact in any college level calculus class, by the end of the 1st semester usually students have completely forgotten how to do even the limit definition of a derivative, let alone the way that that the derivative was developed, because there are all these little tricks and patterns that were discovered that would make this process much quicker to compute by hand (For example: The power rule, the quotient rule etc).
I really agree with this part, I don’t think most of our class really understand what a derivative is and how to get there, myself included, possibly. With the limit definition of a derivative you mean for example how you get from
X³to3X²? If that’s so, it’s one of the things they taught us the less, that didn’t even entered in the test, whenever we needed to derivative we just used the rules you mention.Well Archimedes is really the one who came up with the method of exhaustion, which was later developed into the infinite series, but the main contention to Leibniz and Newton and their infinitesimal from the mathematics community at the time was really that they could use the method of exhaustion and the infinite series to compute very close estimates and that these involved purely numbers, so why bother with this infinitesimal thing that doesn’t even really appear to be mathematics?
Isn’t this also a bit related to integrals? Since you are always working with abstract ideas in order to calculate the area of a surface. I haven’t worked with any integrals, though, just know what they are and they will teach it to me at the beginning of this year.
Honestly it’s very impressive that you have even begun asking the questions at such an early stage. This level of curiosity will absolutely serve you well. I would certainly caution you that the way mathematics is presented at first seems to give it the impression that it is really for calculating numbers that we need in engineering or science. But the reality is that, computers pretty much do all of that for us pretty well. So what actual use is it to learn mathematics? Well, I believe that I’ve made a pretty good case for using towards the dialectical development of knowledge in the total system of science with mathematics playing the role of developing conceptualizations to propel forward the sciences, and using the sciences to propel it forward as well, and that of course can come from an engineer just the same as a scientist. In fact in some sense, engineering is the born synthesis of a mathematician and a scientist, and the first step in orienting scientists and mathematicians towards where they should focus their efforts.
Thanks a lot for the good words, but I wish curiosity alone would produce better results, I drop out of high school and I was taught terribly at it so I’m struggling a lot, plus they basically told us “You already know x, y, z concepts” so I had to study some other stuff (which are basic, but I didn’t know them) on my own, and our physics teacher was the worst, she basically got mad at us because we didn’t understand physics… So yeah. Basically what you are saying is that mathematics serves to understand philosophy rather than numbers, lol. At least it works to understand the ideas behind how reality is structured, with which together with dialectical materialism can provide a huge tool to understand systems and concepts.
Oh thank you for the warm welcome. I’ve been a lurker for awhile and always loved the quality of discussions here, so finally decided to make an account. Also at the end of the day we’re both also comrades and are on equal ground, and in a real sense the process of discussion on this has helped me learn about this in deeper ways too, so sincerely thank you for posting this thread. I think it was Fanon who talks about how the teacher is a student and I just just hope that this very long response may be of use to you or anyone else.
Well, good thing I created this post, then, lol. My Systema teacher (Russian martial arts) always tells me “Estudiante siempre, maestro a veces” (“Student always, teacher sometimes”) so I’m glad I also managed to give you something in return for your time invested.
Marx’s economic and political writings are still relevant, I’m sure his mathematics are on point too. I’m not a mathematician and to be honest you’re the first Marxist I’ve seen who is. So with that I say I can’t help you but thank you for existing, please maintain and further develop because math is very beneficial 👍



